PHIL1009 - Chapter Six
Categorical Propositions
Chapter Overview
Following our discussion of logical reasoning and fallacies in Chapter Five, this chapter delves into the specifics of categorical propositions. We will examine their standard forms, components, and attributes (quality, quantity, distribution). Key topics include understanding immediate inferences, distinguishing between the modern (Boolean) and traditional (Aristotelian) squares of opposition, evaluating inferences using Venn diagrams and the squares of opposition, and exploring logical operations like conversion, obversion, and contraposition.
Chapter Objectives
Upon successful completion of this chapter, you will be able to:
- Define a categorical proposition.
- Identify and explain the four standard forms of categorical propositions (A, E, I, O).
- Explain the attributes of categorical propositions: quality, quantity, and distribution.
- Understand and evaluate immediate inferences using conversion, obversion, and contraposition.
- Describe the logical relationships between propositions illustrated by the traditional and modern squares of opposition.
- Utilize Venn diagrams to represent categorical propositions and test immediate inferences.
1: General Introduction
Section Overview:
Previous chapters provided foundational concepts. Now, we focus specifically on categorical propositions—statements that relate two classes or categories.
These classes are represented by the subject term and the predicate term. A categorical proposition asserts a relationship between these two classes, stating whether all or part of the subject class is included in or excluded from the predicate class. In simpler terms, it's a statement about how two groups or categories relate regarding inclusion or exclusion.
Section Objectives:
Objectives:
After completing this section, you will be able to:
- Understand the definition of a categorical proposition.
- Recognize the standard components of categorical propositions.
- Appreciate the key differences between the traditional (Aristotelian) and modern (Boolean) interpretations and their respective squares of opposition.
What are Categorical Propositions?
A category here refers to a class or set of things (e.g., human beings, animals, plants, students). A proposition, as used in logic, essentially refers to the meaning or information content of a declarative statement (one that can be true or false). For simplicity, we will often use "statement" and "proposition" interchangeably.
Thus, a categorical proposition is a statement asserting a relationship (inclusion or exclusion, partial or whole) between two categories or classes, designated as the subject class and the predicate class.
Examples:
- Every human being is mortal. (Whole subject class included in predicate class)
- No human is eternal. (Whole subject class excluded from predicate class)
- There exists a fish that is a shark. (Equivalent to: Some fish are sharks - Part of subject class included)
- There are plants which are not edible. (Equivalent to: Some plants are not edible things - Part of subject class excluded)
The Need for Standard Form
While the examples on the previous slide express categorical relationships, their phrasing can vary ("Every...," "Nothing that is...," "There exists..."). This variability can make logical analysis difficult. Problems arise in determining:
- The precise quantity (all or some) of the subject class involved.
- The exact nature of the relationship (inclusion or exclusion).
- The overall quality (affirmative or negative) of the assertion.
- Clear logical relationships with other propositions.
To address these issues and facilitate rigorous logical analysis (like determining validity and identifying fallacies), we express categorical propositions in a fixed, unambiguous standard form.
A standard-form categorical proposition clearly expresses one of the four possible relationships between two classes:
The Four Standard Forms
Since any categorical proposition asserts that either all or part of the subject class (S) is included in or excluded from the predicate class (P), there are exactly four standard forms:
-
A Proposition (Universal Affirmative): Asserts that the *whole* subject class is *included* in the predicate class.
Form: All S are P. -
E Proposition (Universal Negative): Asserts that the *whole* subject class is *excluded* from the predicate class.
Form: No S are P. -
I Proposition (Particular Affirmative): Asserts that *part* (at least one member) of the subject class is *included* in the predicate class.
Form: Some S are P. -
O Proposition (Particular Negative): Asserts that *part* (at least one member) of the subject class is *excluded* from the predicate class.
Form: Some S are not P.
These four forms provide a clear, consistent structure for analyzing categorical relationships.
1.2 The Components of Categorical Propositions
Reminder: We use "proposition" and "statement" interchangeably here when referring to categorical assertions.
A standard-form categorical proposition always relates two classes (subject class and predicate class) and has four essential components arranged in a specific order:
- Quantifier: Indicates the quantity of the subject class involved ("All," "No," or "Some").
- Subject Term (S): The term denoting the first class or category.
- Copula: The linking verb connecting the subject and predicate terms ("are" or "are not").
- Predicate Term (P): The term denoting the second class or category.
Standard Order of Components
The correct order for a standard-form categorical proposition is always:
Consider the example:
All members of the Ethiopian Medical Association are people holding degrees from recognized academic institutions.
Analyzing its components:
Components Example Analysis
"All members of the Ethiopian Medical Association are people holding degrees from recognized academic institutions."
Quantifier: All
Subject term (S): members of the Ethiopian Medical Association
Copula: are
Predicate term (P): people holding degrees from recognized academic institutions
A proposition is in standard form if and only if it matches one of the four structures:
- All S are P.
- No S are P.
- Some S are P.
- Some S are not P.
Standard Form Meaning and the Quantifier 'Some'
Symbolically, the meaning of the standard forms in terms of class membership is:
All S are P = Every member of S is also a member of P.
No S are P = No member of S is a member of P.
Some S are P = At least one member of S is also a member of P.
Some S are not P = At least one member of S is not a member of P.
Example Analysis:
Some businesses are not profitable ventures.
Quantifier: Some
Subject term (S): businesses
Copula: are not
Predicate term (P): profitable ventures
Standard form: Some S are not P.
2: Attributes of Categorical Propositions: Quality, Quantity, and Distribution
Section Overview:
Every standard-form categorical proposition possesses three key attributes that determine its logical properties: Quality, Quantity, and the Distribution of its terms. Understanding these attributes is essential for analyzing logical relationships between propositions and evaluating arguments containing them.
Section Objectives:
Objectives:
After completing this section, you will be able to:
- Define and identify the Quality (affirmative/negative) of a categorical proposition.
- Define and identify the Quantity (universal/particular) of a categorical proposition.
- Define and identify the Distribution status (distributed/undistributed) of the subject and predicate terms in each standard form.
- Recognize the standard letter names (A, E, I, O) for the four forms and their associated attributes.
Attribute 1: Quality
- Why are standard letter names (A, E, I, O) useful in logic?
- What are the four essential components of a standard-form categorical proposition?
A. Quality
Quality refers to whether the proposition *affirms* or *denies* class membership (inclusion or exclusion) between the subject and predicate terms.
• If the proposition affirms some kind of class inclusion (either whole or partial), its quality is affirmative.
• If the proposition denies class inclusion (either whole or partial), its quality is negative.
The quality is typically determined by the copula:
| Standard Form | Copula | Quality |
|---|---|---|
| All S are P | are | Affirmative |
| No S are P | are (in "No...are") | Negative |
| Some S are P | are | Affirmative |
| Some S are not P | are not | Negative |
Attribute 2: Quantity
B. Quantity
Quantity refers to whether the proposition makes a claim about *all* members or only *some* (at least one) members of the class designated by the subject term.
• If the proposition makes a claim about every member of the subject class, its quantity is universal.
• If the proposition makes a claim about at least one member of the subject class, its quantity is particular.
The quantity is determined by the quantifier:
| Standard Form | Quantifier | Quantity |
|---|---|---|
| All S are P | All | Universal |
| No S are P | No | Universal |
| Some S are P | Some | Particular |
| Some S are not P | Some | Particular |
Standard Letter Names (A, E, I, O)
Based on their quality and quantity, medieval logicians assigned standard letter names to the four forms, derived from the Latin words *AffIrmo* (I affirm) and *nEgO* (I deny). These letters simplify analysis and discussion:
- A Proposition: Universal Affirmative (from AffIrmo)
- E Proposition: Universal Negative (from nEgO)
- I Proposition: Particular Affirmative (from AffIrmo)
- O Proposition: Particular Negative (from nEgO)
| Form | Letter Name | Quantity | Quality |
|---|---|---|---|
| All S are P | A | Universal | Affirmative |
| No S are P | E | Universal | Negative |
| Some S are P | I | Particular | Affirmative |
| Some S are not P | O | Particular | Negative |
Using these letter names saves time and simplifies logical operations.
Practice with Letter Names
-
Write an example of an "O" proposition:
Example: Some students are not athletes.
Your example: ___________________________________________
-
Fill in the blanks with “same” or “different”:
A. Propositions A and I have the same quality and different quantity.
B. Propositions E and O have the same quality and different quantity.
-
Complete the table:
Standard Form Letter Name Some S are P I No S are P E Some S are not P O All S are P A
Attribute 3: Distribution
C. Distribution
Distribution refers to whether a proposition makes a claim about *every* member of the class designated by a term (subject or predicate).
• A term is distributed if the proposition asserts something about *all* members of the class denoted by that term.
• A term is undistributed if the proposition does *not* assert something about all members of the class denoted by that term (it might assert something about some, or make no claim about the members specifically).
Distribution status for each term in the standard forms:
| Form (Letter Name) | Subject Term (S) | Predicate Term (P) |
|---|---|---|
| A (All S are P) | Distributed | Undistributed |
| E (No S are P) | Distributed | Distributed |
| I (Some S are P) | Undistributed | Undistributed |
| O (Some S are not P) | Undistributed | Distributed |
Mnemonic: Universals (A, E) distribute Subjects. Negatives (E, O) distribute Predicates.
Summary Table of Attributes
The attributes of the four standard-form categorical propositions are summarized below:
| Letter Name | Standard Form | Quality | Quantity | Distributed Terms |
|---|---|---|---|---|
| A | All S are P | Affirmative | Universal | S only |
| E | No S are P | Negative | Universal | S and P |
| I | Some S are P | Affirmative | Particular | None |
| O | Some S are not P | Negative | Particular | P only |
Determining Attributes: Example
Let's determine the attributes for the proposition: "Some birds are mammals."
Standard Form: Some S are P
Letter Name: I
Quality: Affirmative (it affirms inclusion)
Quantity: Particular (it refers to "Some," i.e., at least one)
Distribution:
Subject Term ("birds"): Undistributed (claim is only about *some* birds)
Predicate Term ("mammals"): Undistributed (claim doesn't refer to *all* mammals)
3: Venn Diagrams and the Modern Square of Opposition
Section Overview:
Having defined standard-form categorical propositions, we now explore ways to represent their logical content visually using diagrams and to understand the necessary logical relationships between them. Venn diagrams, developed by John Venn, use overlapping circles to represent the classes denoted by the terms and illustrate the information conveyed by the proposition. The Square of Opposition is a traditional diagram illustrating logical relationships (like contradiction) between the four standard forms.
This section focuses on constructing Venn diagrams for categorical propositions and understanding the Modern Square of Opposition, which reflects the interpretation of categorical propositions adopted in modern logic (often called the Boolean interpretation).
Section Objectives:
Objectives:
After completing this section, you will be able to:
- Understand the purpose and basic conventions of Venn diagrams for categorical propositions.
- Represent each of the four standard-form propositions (A, E, I, O) using Venn diagrams.
- Understand and apply the Modern Square of Opposition to determine logical relationships (contradiction) between propositions.
3.1 Representing Categorical Propositions in Venn Diagrams
Why might representing propositions visually in a diagram be useful in logic?
Venn diagrams provide a visual method for representing the information contained in categorical propositions. For a single proposition with two terms (Subject S and Predicate P), the diagram consists of two overlapping circles, each representing a class. The overlap area represents members belonging to *both* classes. The areas outside the overlap represent members belonging to one class but *not* the other.
By convention, the left circle typically represents the Subject (S) class, and the right circle represents the Predicate (P) class.
Venn Diagram Conventions
Specific conventions are used to represent the claims made by standard-form propositions:
- Shading an area indicates that the area is empty—it contains no members. Universal propositions (A and E), which deny the existence of certain kinds of members, are represented using shading.
- Placing an X in an area indicates that the area is not empty—it contains at least one member. Particular propositions (I and O), which assert existence, are represented using an X.
- If an area is left blank (neither shaded nor containing an X), no information is known about its membership—it could be empty or occupied.
Let's diagram each standard form.
Diagramming A and E Propositions
1. A Proposition: All S are P
Meaning: Every member of S is in P. Thus, the part of S *outside* P must be empty.
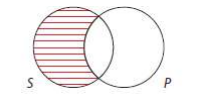
Shade the area of S that is outside P.
2. E Proposition: No S are P
Meaning: No member of S is in P. Thus, the area where S and P *overlap* must be empty.
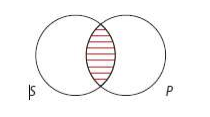
Shade the area of overlap between S and P.
Diagramming I and O Propositions
3. I Proposition: Some S are P
Meaning: At least one member of S is also a member of P. Thus, the overlap area is *not* empty.
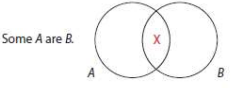
Place an X in the area of overlap between S and P.
4. O Proposition: Some S are not P
Meaning: At least one member of S is *not* a member of P. Thus, the part of S *outside* P is *not* empty.

Place an X in the area of S that is outside P.
3.2 The Modern Square of Opposition
Comparing the Venn diagrams reveals necessary logical relationships between the standard-form propositions.
• Compare A (All S are P) and O (Some S are not P): The A diagram shades the left part of S (empty). The O diagram places an X in the *same* area (not empty). These diagrams make opposite claims about the same region.
• Compare E (No S are P) and I (Some S are P): The E diagram shades the overlap area (empty). The I diagram places an X in the *same* area (not empty). These also make opposite claims.
Propositions making opposite claims cannot both be true and cannot both be false; they must have opposite truth values. This relationship is called contradiction.
The Modern Square of Opposition (based on the Boolean interpretation, which makes no assumptions about existence) primarily illustrates this contradictory relationship.
The Modern Square of Opposition Diagram
The diagram visually represents the relationship between corresponding A, E, I, and O propositions with the same subject and predicate terms:
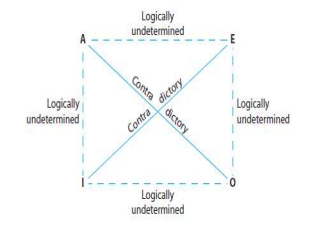
The diagonal lines indicate the contradictory relationship:
- A and O propositions are contradictories.
- E and I propositions are contradictories.
Contradictories always have opposite truth values. If one is true, the other must be false, and vice versa.
Using the Modern Square for Immediate Inferences
The necessary relationships shown on the square allow us to make immediate inferences—arguments with only one premise. If we know the truth value of one proposition, we can immediately infer the truth value of its contradictory.
To test the validity of an immediate inference using the modern square:
- Assume the premise is true.
- Determine the truth value of the conclusion based *only* on the contradictory relationship shown on the square.
- If the conclusion's truth value matches what the square dictates, the inference is valid (from the Boolean standpoint). If it doesn't match, or if the square provides no information (for relationships other than contradictory), the inference is invalid.
Example Inference:
Premise: It is true that Some S are P. (I is True)
Conclusion: Therefore, it must be false that No S are P. (E is False)
Analysis: If I is true, its contradictory E must be false. The conclusion asserts E is false. Therefore, the inference is valid according to the modern square.
3.3 The Traditional Square of Opposition
Historically, logic (following Aristotle) interpreted universal propositions (A and E) differently than modern logic. The Aristotelian standpoint assumes that universal propositions about existing things have existential import—meaning they imply that the classes they refer to (S and P) actually have members. The modern Boolean interpretation makes no such assumption.
This assumption of existential import for universal propositions allows for more logical relationships than just contradiction. These additional relationships are captured in the Traditional Square of Opposition.
The traditional square applies *only* when we assume that the subject terms of A and E propositions denote classes that are not empty (i.e., that members exist).
The Traditional Square of Opposition Diagram
Assuming existential import for universal propositions, the traditional square illustrates four relationships:
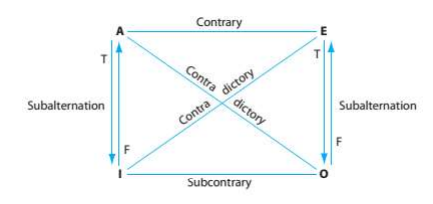
The relationships are Contradictory (diagonals), Contrary (top), Subcontrary (bottom), and Subalternation (sides).
Traditional Square Relationships Defined
Under the Aristotelian interpretation (assuming existence):
- Contradictory (A vs. O, E vs. I): Always have opposite truth values. (Same as modern square).
- Contrary (A vs. E): Cannot both be true, but *can* both be false. (If one is true, the other is false. If one is false, the other is undetermined).
- Subcontrary (I vs. O): Cannot both be false, but *can* both be true. (If one is false, the other is true. If one is true, the other is undetermined).
- Subalternation (A → I, E → O): Truth flows downward (if the universal is true, the particular is true). Falsity flows upward (if the particular is false, the universal is false). Other directions are undetermined.
Contrary and Subcontrary Relationships
Contrary (A vs. E): They express partial opposition.
• If "All cats are animals" (A, True) is given, then "No cats are animals" (E) must be False.
• If "No cats are dogs" (E, True) is given, then "All cats are dogs" (A) must be False.
• However, if "All animals are cats" (A, False) is given, "No animals are cats" (E) could be true or false (it happens to be true, but isn't logically determined just from A being false). They can both be false.
Subcontrary (I vs. O): They also express partial opposition.
• If "Some dogs are cats" (I, False) is given, then "Some dogs are not cats" (O) must be True.
• If "Some cats are not animals" (O, False) is given, then "Some cats are animals" (I) must be True.
• However, if "Some animals are cats" (I, True) is given, "Some animals are not cats" (O) could be true or false (it happens to be true, but isn't logically determined just from I being true). They can both be true.
Subalternation Relationship
Subalternation (A vs. I, E vs. O): This relationship relies heavily on the existential import assumption for A and E.
- Truth Downward: If a universal proposition (A or E) is true, its corresponding particular proposition (I or O) must also be true.
Example: If "All cats are mammals" (A, True) is given, then "Some cats are mammals" (I) must be True. - Falsity Upward: If a particular proposition (I or O) is false, its corresponding universal proposition (A or E) must also be false.
Example: If "Some cats are reptiles" (I, False) is given, then "All cats are reptiles" (A) must be False. - Undetermined Cases: If a universal (A/E) is false, the particular (I/O) is undetermined. If a particular (I/O) is true, the universal (A/E) is undetermined.
Think: Truth trickles down, Falsity floats up.
4: Evaluating Immediate Inferences using Squares and Diagrams
Section Overview:
The squares of opposition and Venn diagrams provide tools for evaluating the validity of immediate inferences—arguments with only one premise and one conclusion, where both are categorical propositions.
This section demonstrates how to use these tools. We will test inferences using the modern square (Boolean interpretation), the traditional square (Aristotelian interpretation, assuming existential import), and Venn diagrams. We will also introduce the concept of the existential fallacy.
Section Objectives:
Objectives:
After completing this section, you will be able to:
- Test the validity of immediate inferences using the Modern Square of Opposition.
- Test the validity of immediate inferences using the Traditional Square of Opposition (conditionally valid arguments).
- Identify the Existential Fallacy from the Boolean perspective.
- Test the validity of immediate inferences using Venn diagrams.
Evaluating Inferences with the Modern Square
Using the modern square (which only shows the contradictory relationship), we test validity as follows:
Example Inference:
Premise: Some trade spies are not masters at bribery. (O is True)
Conclusion: Therefore, it is false that all trade spies are masters at bribery. (A is False)
Steps:
- Assume the premise (O proposition) is True. Enter 'T' by O on the square.
- Use the contradictory relation: If O is True, then A must be False. Enter 'F' by A.
- Compare with the conclusion: The conclusion asserts that A is False ("it is false that all...").
- Since the truth value derived from the square (A is False) matches the conclusion, the argument is valid from the Boolean standpoint.
Unconditional Validity and Negated Statements
Arguments valid solely based on the modern square (contradictory relationship) are unconditionally valid because their validity doesn't depend on whether the terms refer to existing things (no existential import is assumed).
Note on Negated Statements: Conclusions like "It is false that all S are P" are not technically in standard form. For evaluation, we treat them as equivalent to asserting the falsity of the corresponding standard-form proposition (e.g., "'All S are P' is false"). Similarly, "It is false that no S are P" means "'No S are P' is false," and so on.
Evaluating Inferences with Venn Diagrams
Venn diagrams offer another method. To test validity:
- Draw separate Venn diagrams for the premise and the conclusion.
- If the information shown in the conclusion diagram is *already contained* within the premise diagram, the inference is valid.
- If the conclusion diagram contains information *not* present in the premise diagram, the inference is invalid.
Diagramming Negated Statements:
- "It is false that All A are B" (False A) means the same as "Some A are not B" (O). Diagrammed with an X in the left part of A.
- "It is false that No A are B" (False E) means the same as "Some A are B" (I). Diagrammed with an X in the overlap.
- "It is false that Some A are B" (False I) means the same as "No A are B" (E). Diagrammed by shading the overlap.
- "It is false that Some A are not B" (False O) means the same as "All A are B" (A). Diagrammed by shading the left part of A.
Venn Diagram Validity Example
Let's test the previous inference using Venn diagrams:
Premise: Some T are not M. (O Proposition)
Conclusion: Therefore, it is false that all T are M. (Equivalent to O Proposition)
Diagrams:
Premise: Some T are not M (O)

Conclusion: False(All T are M) => Some T are not M (O)

Both premise and conclusion are represented by placing an X in the part of the T circle outside the M circle. Since the information in the conclusion diagram (an X in that region) is identical to the information in the premise diagram, the inference is valid.
Venn Diagram Invalidity & The Existential Fallacy
Consider this inference using the traditional square's subalternation:
Premise: All C are H. (A Proposition)
Conclusion: Therefore, Some C are H. (I Proposition)
Diagrams (Boolean Interpretation):
Premise: All C are H (A)

Conclusion: Some C are H (I)

The premise diagram (shaded left part of C) does *not* contain the information in the conclusion diagram (an X in the overlap). The premise makes no claim about existence, while the conclusion does. Therefore, from the Boolean standpoint, this inference is invalid.
This specific type of invalidity—where an argument is invalid *merely* because it moves from a universal premise (lacking existential import) to a particular conclusion (having existential import)—commits the Existential Fallacy.
Conditionally Valid Arguments
Arguments that commit the existential fallacy from the Boolean standpoint *can* be valid from the Aristotelian standpoint, *if* we make the required assumption that the subject term denotes existing things. Such arguments are termed conditionally valid—valid on the condition of existence.
Inferences based on the traditional square relationships of contrary, subcontrary, and subalternation are often conditionally valid. They are valid only if the relevant classes (subject terms of A/E) are assumed to have members.
Examples of forms that commit the existential fallacy (invalid Booleanly, conditionally valid Aristotelianly):
- All A are B. Therefore, Some A are B. (Subalternation)
- No A are B. Therefore, Some A are not B. (Subalternation)
- It is false that Some A are not B (i.e., All A are B). Therefore, it is false that No A are B (i.e., Some A are B). (Contradictory + Subalternation)
- It is false that Some A are B (i.e., No A are B). Therefore, Some A are not B. (Contradictory + Subalternation)
To detect the existential fallacy, check if an argument moves from universal premise(s) to a particular conclusion *and* if its invalidity stems *only* from the lack of existential import in the premise(s). Venn diagrams clearly show this mismatch.
4.1 Logical Operations: Conversion, Obversion, and Contraposition
Beyond the relationships shown on the squares of opposition, we can analyze immediate inferences based on three specific logical operations performed on standard-form categorical propositions: Conversion, Obversion, and Contraposition.
These operations manipulate the terms or quality of a proposition to create a new proposition. We can then determine if the new proposition is logically equivalent to the original (meaning they always have the same truth value) and whether an immediate inference from the original to the new proposition is valid. Venn diagrams are useful here.
Operation 1: Conversion
Conversion involves switching the subject term (S) and the predicate term (P).
Applying conversion to the four standard forms yields:
| Form | Given Proposition | Converse (Switch S and P) |
|---|---|---|
| A | All S are P | All P are S |
| E | No S are P | No P are S |
| I | Some S are P | Some P are S |
| O | Some S are not P | Some P are not S |
The new statement formed is called the converse of the original.
Venn Diagrams for Conversion (A & E)
Comparing Venn diagrams for propositions and their converses helps determine logical equivalence:
Given A: All S are P

Converse: All P are S
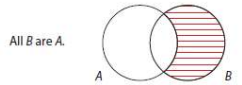
Diagrams are different. A and its converse are *not* logically equivalent.
Given E: No S are P

Converse: No P are S
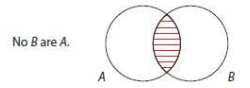
Diagrams are identical. E and its converse *are* logically equivalent.
Venn Diagrams for Conversion (I & O)
Given I: Some S are P

Converse: Some P are S
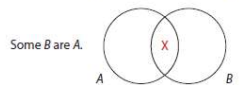
Diagrams are identical. I and its converse *are* logically equivalent.
Given O: Some S are not P

Converse: Some P are not S
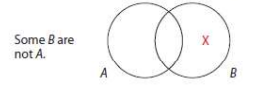
Diagrams are different. O and its converse are *not* logically equivalent.
Validity of Conversion
Based on the Venn diagrams (and logical equivalence):
- Conversion is valid for E and I propositions. This means an E proposition always has the same truth value as its converse, and an I proposition always has the same truth value as its converse. Immediate inferences are valid:
(No S are P ∴ No P are S) and (Some S are P ∴ Some P are S). - Conversion is invalid for A and O propositions. Their truth values are logically unrelated to their converses. Immediate inferences are invalid:
(All S are P ∴ All P are S) and (Some S are not P ∴ Some P are not S).
Example (Valid E Conversion):
Premise: No birds are featherless things. (True)
Conclusion: Therefore, no featherless things are birds. (True - Valid)
Example (Valid I Conversion):
Premise: Some businesses are profitable ventures. (True)
Conclusion: Therefore, some profitable ventures are businesses. (True - Valid)
Illicit Conversion Fallacy
Since conversion is invalid for A and O propositions, attempting to infer the converse from an A or O statement commits the formal fallacy of Illicit Conversion.
Invalid Forms (Illicit Conversion):
All A are B.
Therefore, all B are A.
Some A are not B.
Therefore, some B are not A.
Examples of Illicit Conversion:
All cats are animals. (True) → Therefore, all animals are cats. (False)
Some animals are not dogs. (True) → Therefore, some dogs are not animals. (False)
The truth of the premise does not guarantee the truth of the conclusion in these forms.
Operation 2: Obversion
Obversion is a two-step operation:
- Change the quality: Affirmative becomes negative, negative becomes affirmative. (A ↔ E, I ↔ O). The quantity (universal/particular) remains the same.
- Replace the predicate term with its term complement: Replace P with non-P. The term complement refers to the class of everything outside the original term's class (e.g., complement of "dogs" is "non-dogs"; complement of "voters" is "non-voters").
The resulting statement is called the obverse.
Obversion Applied to Standard Forms
Applying the two steps (change quality, replace P with non-P):
| Form | Given Proposition | Obverse |
|---|---|---|
| A | All S are P | No S are non-P |
| E | No S are P | All S are non-P |
| I | Some S are P | Some S are not non-P |
| O | Some S are not P | Some S are non-P |
Venn Diagrams for Obversion (A & E)
Comparing diagrams for propositions and their obverses:
Given A: All S are P

Obverse: No S are non-P
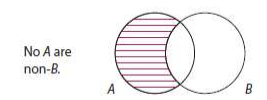
Given E: No S are P

Obverse: All S are non-P
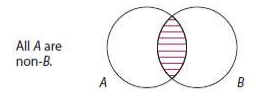
Venn Diagrams for Obversion (I & O)
Given I: Some S are P

Obverse: Some S are not non-P
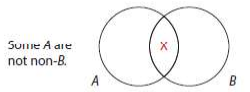
Given O: Some S are not P

Obverse: Some S are non-P
Validity of Obversion
As the identical Venn diagrams demonstrate, obversion produces a logically equivalent proposition for *all four* standard forms (A, E, I, O).
Therefore, obversion is always valid for all four types of categorical propositions. An immediate inference from any standard-form proposition to its obverse is always valid.
Examples (Valid Obversion):
All S are P ∴ No S are non-P
No S are P ∴ All S are non-P
Some S are P ∴ Some S are not non-P
Some S are not P ∴ Some S are non-P
If the premise is true, the obverse conclusion must also be true.
Operation 3: Contraposition
Contraposition is also a two-step operation:
- Switch the subject and predicate terms (like conversion).
- Replace *both* the (new) subject term and the (new) predicate term with their term complements.
The resulting statement is called the contrapositive.
Applying these steps:
| Form | Given Proposition | Contrapositive |
|---|---|---|
| A | All S are P | All non-P are non-S |
| E | No S are P | No non-P are non-S |
| I | Some S are P | Some non-P are non-S |
| O | Some S are not P | Some non-P are not non-S |
Venn Diagrams for Contraposition (A & E)
Comparing diagrams for propositions and their contrapositives:
Given A: All S are P

Contrapositive: All non-P are non-S
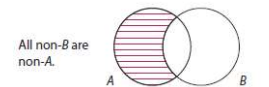
Diagrams are identical. A and its contrapositive *are* logically equivalent.
Given E: No S are P

Contrapositive: No non-P are non-S
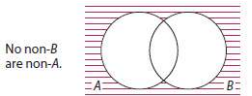
Diagrams are different. E and its contrapositive are *not* logically equivalent (Booleanly).
Venn Diagrams for Contraposition (I & O)
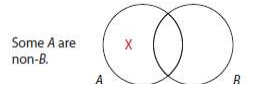
Given I: Some S are P

Contrapositive: Some non-P are non-S
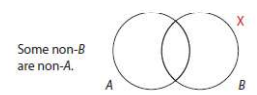
Diagrams are different. I and its contrapositive are *not* logically equivalent.
Given O: Some S are not P

Contrapositive: Some non-P are not non-S
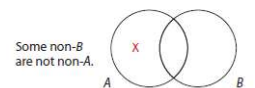
Diagrams are identical. O and its contrapositive *are* logically equivalent.
Validity of Contraposition
Based on the Venn diagrams (and logical equivalence under Boolean interpretation):
- Contraposition is valid for A and O propositions. They always have the same truth value as their contrapositives. Immediate inferences are valid:
(All S are P ∴ All non-P are non-S) and (Some S are not P ∴ Some non-P are not non-S). - Contraposition is invalid for E and I propositions (from the Boolean standpoint). Their truth values are not necessarily the same as their contrapositives. However, E by contraposition *can be valid if existential import is assumed for S*.
Example (Valid A Contraposition):
Premise: All worshippers are believers. (True)
Conclusion: Therefore, all non-believers are non-worshippers. (True - Valid)
Illicit Contraposition Fallacy
Since contraposition is generally invalid for E and I propositions (from the Boolean perspective), attempting to infer the contrapositive from such statements commits the formal fallacy of Illicit Contraposition.
Invalid Forms (Illicit Contraposition - Boolean):
No A are B.
Therefore, no non-B are non-A.
Some A are B.
Therefore, some non-B are non-A.
Examples of Illicit Contraposition:
No dogs are cats. (True) → Therefore, no non-cats are non-dogs. (False - e.g., a bird is a non-cat but not a non-dog).
Some animals are non-cats (e.g., dogs). (True) → Therefore, some cats are non-animals. (False - all cats are animals).
Both Illicit Conversion and Illicit Contraposition are formal fallacies, detectable by examining the argument's form.
Chapter Summary
A categorical proposition relates two classes (subject S and predicate P), asserting full or partial inclusion or exclusion. The four standard forms (A, E, I, O) have specific Quality (affirmative/negative), Quantity (universal/particular), and term Distribution patterns. Venn diagrams visualize these forms (shading=empty, X=not empty).
The Modern Square of Opposition shows the contradictory relationship (A/O, E/I always opposite truth values). The Traditional Square adds contrary (A/E not both true), subcontrary (I/O not both false), and subalternation (truth down, falsity up) relationships, assuming existential import for A/E propositions. These squares and Venn diagrams test immediate inferences. Arguments invalid solely due to lacking existential import commit the Existential Fallacy (Boolean view).
Logical operations transform propositions: Conversion (switch S/P; valid for E/I), Obversion (change quality, complement P; valid for A/E/I/O), Contraposition (switch S/P, complement both; valid for A/O, and for E if existential import is assumed for S). Invalid operations result in formal fallacies (Illicit Conversion/Contraposition).
Self-Check Exercises
- Why is expressing categorical propositions in standard form important for logical analysis?
- What potential problems arise if categorical propositions are not analyzed in standard form?
- Provide an example of an E proposition (No S are P).
- Write the O proposition with "soldiers" as the subject term and "cowards" as the predicate term.
- Symbolically represent the meaning of an I proposition ("Some S are P").
- Explain why "All S are not P" is not a standard-form categorical proposition. (Hint: Consider the copula).
- Provide an example of an A proposition (All S are P).
Self-Check Exercises (Continued)
I. Draw Venn diagrams for the following propositions:
- Some rock-music lovers are not fans of Madonna. (O)
- All S are non-P. (Equivalent to E: No S are P)
- Some housing developments are complexes that exclude children. (I)
II. Use the modern square of opposition to determine validity (Boolean standpoint):
-
Premise: Some country doctors are altruistic healers. (I)
Conclusion: Therefore, some country doctors are not altruistic healers. (O) -
Premise: It is false that all weddings are light-hearted celebrations. (False A / True O)
Conclusion: Therefore, some weddings are not light-hearted celebrations. (O)
Self-Check Exercises (Continued)
III. Perform Conversion on the following. Is the converse logically equivalent?
- All hurricanes are storms intensified by global warming. (A)
- No sex-change operations are completely successful procedures. (E)
IV. Perform Obversion on the following. Is the obverse logically equivalent?
- All radically egalitarian societies are societies that do not preserve individual liberties. (A)
- No cult leaders are people who fail to brainwash their followers. (E)
V. Perform Contraposition on the following. Is the contrapositive logically equivalent?
- Some popular television programs are not intellectually stimulating entertainments. (O)
- All physicians whose licenses have been revoked are physicians ineligible to practice. (A)
References
- Copi, I. M., & Cohen, C. (1990). Introduction to Logic. Macmillan Publishing Company.
- Damer, T. E. (2005). Attacking Faulty Reasoning: A Practical Guide to Fallacy-Free Arguments. Wadsworth Cengage learning.
- Fogelin, R. J. (1987). Understanding Arguments: An Introduction to Informal Logic. Harcourt Brace Jovanovich Publisher.
- Gensler, H. J. (2010). Introduction to Logic (2nd ed.). Routledge.
- Guttenplan, S. (1991). The Language of Logic. Blackwell Publishers.
- Howard-Snyder, F., Howard-Snyder, D., & Wasserman, R. (2012). The Power of Logic (5th ed.). McGraw-Hill.
- Hurley, P. J. (2006). A Concise Introduction to Logic (9th ed.). Wadsworth/Thomson Learning.
- Hurley, P. J. (2012). A Concise Introduction to Logic (11th ed.). Wadsworth, Cengage Learning.
- Hurley, P. J. (2014). A Concise Introduction to Logic (12th ed.). Wadsworth, Cengage Learning.
- Simco, N. D., & James, G. G. (1983). Elementary Logic. Wadsworth Publishing Company.
- Stephen, C. (2000). The Power of Logic. Mayfield Publishing Company.
- Walelign, Emuru. (2009). Freshman Logic. Addis Ababa.
- Walton, D. N. (2006). Fundamentals of Critical Argumentation. Cambridge University Press.